Глава 1 ОСНОВНІ МЕТРОЛОГІЧНІ ПОНЯТТЯ СТОСОВНО ФІЗИЧНИХ ВЕЛИЧИН ТА ОДИНИЦЬ. ТЕОРІЯ РОЗМІРНОСТЕЙ

Зміст глави 1

1.1 Загальні відомості про фізичні величини та їх вимірювання. Уявлення про метрологію

1.2 Основні та похідні фізичні величини й одиниці. Розмірності фізичних величин

1.3 Принцип однорідності щодо розмірностей. П –теорема

1.4 Методи фізичних досліджень, які ґрунтуються на аналізі  розмірностей. Доповнення Хантлi

1.5 Зведення основних практичних правил теорії розмірностей

Зміст      1.1 Загальнi вiдомостi про фiзичнi величини та  їх вимiрювання. Уявлення про метрологiю

Багато сфер дiяльностi людини та суспiльства тiсно пов’язанi з вимiрюванням фiзичних величин та їх вираженням через вiдповiднi одиницi.

Фiзичною величиною (величиною)  [1]  називається властивiсть, спiльна в якісному вiдношеннi для багатьох фiзичних об’єктiв та iндивідуальна в кiлькiсному вiдношеннi для кожного з них. Під індiвiдуальнiстю розумiєється, що властивiсть, притаманна одному об’єкту, може у визначену кiлькiсть разiв перевищувати або бути меншою порівняно з властивістю іншого об’єкта.

Якісна означеність фізичної величини визначає її рід, а величини з однаковою якісною означеністю є однорідними. Наприклад, такі величини, як довжина, ширина, висота, діаметр, шлях, довжина хвилі - однорідні, оскільки їхні якісні означеності збігаються.

Кількісний вміст фізичної величини в даному об’єкті є розміром (фізичної) величини. Якiсна та кiлькiсна сторони фiзичної величини нерозривно пов’язані мiж собою. З метою запобігти тавтології термiн "величина" не слiд використовувати як кількісну характеристику даної властивості. Не можна, наприклад, писати "величина маси", "величина напруги", "величина магнітної iндукції", тому що маса, напруга та магнiтна iндукцiя самi є величинами. У таких випадках доречними будуть терміни "розмір маси", "розмір напруги", "розмір магнітної індукції".

Числовим значенням (фізичної) величини називається число, що дорівнює відношенню розміру фізичної величини, що вимірюється, до розміру одиниці цієї фізичної величини, чи кратної (частинної) одиниці.

Значенням (фiзичної) величини називається відображення фiзичної величини у виглядi числового значення величини з позначенням її одиниці. Значення фiзичної величини можна отримати, як результат обчислення або вимiрювання.

Істинним значенням (фiзичної величини) називається значення фізичної величини, яке iдеально вiдображало б певну властивiсть об’єкта.

Умовно істинним значенням (фізичної величини), або дiйсним значенням (фiзичної величини), називається значення фiзичної величини, знайдене експериментальним шляхом i настiльки наближене до істинного значення, що його можна використати замість істинного для даної мети.

Вимiрюванням називається відображення вимірюваних величин їх значеннями за допомогою експерименту та обчислень із застосуванням спеціальних технічних засобів.

Вимiрюють фiзичні величини, використовуючи вiдповiднi фiзичнi явища. Сукупнiсть фiзичних явищ, що лежать в основi вимiрювань, називається принципом вимiрювань. Наприклад, температуру вимiрюють з використанням термоелектричного ефекту, масу  – зважуванням (використання сили тяжiння, що пропорцiйна до маси), витрату газу або рiдини – за перепадом тиску тощо.

Результати вимірювань можуть бути використані за умови, якщо відомі відповідні характеристики похибок вимірювань. Для цього треба добрати правильну методику виконання вимірювань, тобто сукупність процедур і правил, виконання яких забезпечує одержання результатів вимірювань з потрібною точністю.

Вимiрювання фiзичних величин дуже важливi для вирiшення рiзноманiтних наукових i практичних завдань. Зокрема, вимiрюючи фiзичні величини, що характеризують той чи iнший об’єкт, можна встановити та кiлькiсно виразити iснуючі мiж ними зв’язки. Саме в такий спосіб було встановлено зв’язок мiж масою тiла, прискоренням та силою, що його спричинює (другий закон Ньютона); зв’язок мiж силою струму, напругою на дiлянцi кола та її опором (закон Ома) та ін.

Неодмiнною умовою виконання вимiрювань є вибiр одиниць вiдповiдних фiзичних величин. Цей вибір грунтується на тому, що однорідні величини можна порівнювати між собою.

Одиницею (фiзичної величини) називається фiзична величина певного розміру, прийнята за угодою для кількісного відображення однорідних з нею величин. Одиницi будь-якої величини можуть рiзнитися за розмiром. Так метр, фут і дюйм є одиницями довжини, проте мають рiзний розмiр: 1 фт = 0,3048 м;  1 дюйм = 25,4^.10^-3 м.

Зауважимо, що в Законі "Про метрологію та метрологічну діяльність" подано дещо інше визначення, а саме: одиниця вимірювань – фізична величина певного розміру, прийнята для кількісного відображення однорідних з нею величин. Уведення в згаданому законі терміна "одиниця вимірювань" найвірогідніше пов’язано з наміром його авторів наголосити на ролі вимірювань у науці й техніці. Проте цей термін не узгоджується ані з міжнародними стандартами [8 - 21], ані з міждержавним стандартом [34], ані з чинними стандартами України     [1 - 6]. Тому в даному посібнику (за винятком випадків, коли наводяться прямі посилання на Закон "Про метрологію та метрологічну діяльність")  використовувати­меться фізично й мовно точніший термін "одиниця (фізичної) величини".

Кожна одиниця фiзичної величини має назву, яка може бути спецiальною чи похiдною вiд назв iнших одиниць. Наприклад, спеціальні назви мають такі одиниці, як метр, секунда, джоуль, тесла, а похідні - метр за секунду, джоуль на кілограм, тесла на метр.

Позначення одиниці (фізичної величини) є умовним символом одиниці фізичної величини. Позначення одиниці може бути абревіатурою слів, що входять в її назву, або спеціальним знаком. Згідно з ДСТУ 3651 допустимими до застосування в Україні є позначення міжнародні (з використанням літер латинської чи грецької абеток) та українські (з використанням літер української абетки). Наприклад, 1 метр може позначатися 1 m або 1 м, 1 джоуль на кілограм - 1 J/kg або 1 Дж/кг. До спеціальних знаків, якими позначають одиниці, належать, наприклад, знак ^о термометричного градуса (1 градус Цельсія позначається 1 ^оС), знак % відсотка чи процента (1 відсоток - 1 %),  знаки ...,^о ...', ..." відповідно кутових градуса, хвилини та секунди. Правила, що регламентують утворення, написання та використання позначень одиниць, докладно подано в главі 3.

Якщо зі сукупності однорідних величин виділяється деяка відлікова величина, що умовно називається одиницею, то всі інші однорідні величини можуть бути виражені кількісно в термінах цієї одиниці як добуток одиниці й числа

А = {A}^.[A],            (1.1)

де А - символ величини, {A} - числове значення величини А, вираженої в одиниці [A].

Наприклад, довжина хвилі однієї з ліній спектра натрію l = 5,896^.10^-7 м, де l - символ величини - довжини хвилі; м - позначення одиниці довжини - метра; 5,896^.10^-7 - числове значення довжини хвилі, вираженої в метрах.

Рiвняння (1.1) називається основним рiвнянням вимiрювання. З нього випливає, що результат вимiрювання {A}^.[A] виражатиметься за допомогою одиницi [А]. Числове значення величини дорiвнює вiдношенню мiж фiзичною величиною та вiдповiдною одиницею:

{A} = A/[A].            (1.2)

Значення величини, яке дорівнює добутку її числового значення і одиниці, не залежить від вибору одиниці. Якщо величину виразити в іншій одиниці, що в k разів перевищує першу одиницю, то нове числове значення величини стає в 1/k разів меншим від першого числового значення. Наприклад, у результаті заміни одиниці довжини хвилі з метра на нанометр, який у 10⁹ разів менший від метра, числове значення довжини хвилі збільшиться в 10⁹ разів:

l = 5,896^.10^-7 м = 5,896^.10^-7.10⁹ нм = 589,6 нм. 

Довжина хвилі при цьому не змінюється.

Інколи числове значення величини наводять у такому вигляді: або беручи у фігурні дужки символ величини з використанням одиниці як нижнього індексу, або записуючи відношення між величиною та вибраною одиницею. Наприклад,

{l }_нм = l /нм = 589,6.

Вимiрюють фiзичні величини з допомогою вiдповiдних засобiв вимiрювальної техніки, тобто технiчних засобiв, якi застостовуються пiд час вимiрювань i мають нормованi метрологiчнi характеристики. Тип засобу вимірювальної техніки визначає сукупність засобів вимірювальної техніки одного і того ж призначення, які мають один і той же принцип дії, однакову конструкцію та виготовлені за однією і тією ж технічною документацією

До засобів вимірювальної техніки належать засоби вимірювань та вимірювальні пристрої.

Засіб вимірювань - це засіб вимірювальної техніки, який реалізує процедуру вимірювань, наприклад кодові засоби вимірювань, вимірювальні прилади, вимірювальні канали та вимірювальні системи. В ідеальному випадку засіб вимірювань реалізує лінійну залежність між значенням вимірюваної величини та її відповідними розмірами.

Вимірювальний пристрій - це засіб вимірювальної техніки, в якому виконується лише одна зі складових частин процедури вимірювань (вимірювальна операція). Існують рiзноманiтнi засоби вимiрювань. Серед них особливе мiсце посiдають міри та еталони одиниць.

Пiд мiрою (величини) розумiється вимiрювальний пристрій, що реалізує вiдтворення та (або) збереження фiзичної величини заданого значення. Наприклад, гиря є мiрою маси, вимiрювальний резистор - мiрою електричного опору,  температурна лампа - мiрою яскравiсної або колiрної температури тощо.

Мiри бувають однозначними та багатозначними. Однозначною називають мiру, що вiдтворює фiзичну величину одного розмiру, наприклад гиря, плоско-паралельна кiнцева мiра довжини, вимiрювальний резистор, нормальний елемент. Багатозначною називають мiру, що вiдтворює ряд однойменних величин рiзного розмiру (наприклад, варiометр iндуктивностi, конденсатор змiнної ємностi та ін.).

Еталоном називається засiб вимiрювальної техніки, що забезпечує відтворення і (або) зберігання одиниці вимірювань одного чи декількох значень, а також передачу розміру цієї одиниці іншим засобам вимірювальної техніки.

Прикладами еталонів є платино-iридiєва гиря № 6, затверджена як еталон-копiя кiлограма; група з шести манганiнових резисторiв, затверджена як еталон ома; комплекс засобiв вiдтворення метра з використанням світлової хвилі, затверджений як первiсний еталон метра та ін.

Еталони поділяють на державні, робочі та вихідні.

Державний еталон - це офіційно затверджений еталон, який забезпечує відтворення одиниці вимірювань та передачу її розміру іншим еталонам з найвищою у країні точністю. Державні еталони забезпечують відтворення та зберігання одиниць вимірювань з метою передачі їхніх розмірів засобам вимірювальної техніки, які застосовуються на території України.

Еталонна база створюється та удосконалюється відповідно до державних науково-технічних програм, які розробляються Державним комітетом України по стандартизації, метрології та сертифікації (далі – Держстандарт України) з метою забезпечення потреб економіки і оборони України. За виконання завдань цих програм, технічний рівень державних еталонів та оптимальність структури еталонної бази відповідає Держстандарт України.

Державні еталони є виключно державною власністю, підлягають затвердженню Держстандартом України і перебувають у його віданні. Відповідальність за додержання правил і умов зберігання та застосування державних еталонів покладається на керівників організацій та вчених зберігачів цих еталонів.

 Робочий еталон призначено для повірки чи калібрування засобів вимірювальної техніки, а вихідний  еталон – це такий еталон, який має найвищі метрологічні властивості серед еталонів, що є на підприємстві чи в організації.

Еталони використовують для перевiрки зразкових засобiв вимiрювальної техніки [засобів вимірювання], що, у свою чергу, застосовують для перевiрки з їх допомогою iнших засобiв вимiрювальної техніки, наприклад робочих засобів вимірювань, якi застосовують для вимiрювань, не пов’язаних з передаванням розмiру одиниць.

Засоби вимірювальної техніки можуть застосовуватися, якщо вони відповідають вимогам щодо точності, встановленим для цих засобів, у певних умовах їх експлуатації.

Порядок встановлення приналежності технічних засобів до засобів вимірювальної техніки, визначається Держстандартом України.

Засоби вимірювальної техніки, на які поширюється державний метрологічний нагляд, дозволяється застосовувати, випускати з виробництва, ремонту та у продаж і видавати напрокат лише за умови, якщо вони пройшли повірку або державну метрологічну атестацію (див. підрозд. 3.1).

Ввезення на територію України засобів вимірювальної техніки партіями може здійснюватися, якщо типи цих засобів занесені до державного реєстру засобів вимірювальної техніки (Державного реєстру України), допущених до застосування в Україні. Порядок ввезення на територію України засобів вимірювальної техніки встановлюється Кабінетом Міністрів України.

Iстотне значення має забезпечення єдностi вимiрювань, тобто такого стану вимiрювань, за якого їх результати виражаються в узаконених одиницях вимірювань, а похибки вимiрювань вiдомi та із заданою ймовiрнiстю не виходять за встановлені межі.

Нинi розроблено і класифіковано багато методів вимiрювань, що враховують специфiку  вимiрювання рiзноманiтних фiзичних величин, здiйснено їх класифiкацiю (див. [4]).

Ускладнення вимiрювань і розширення їх рiзноманiтностi зумовили становлення самостiйної галузi науки - метрології (вiд грецьк. метрон - мiра та логос – учення), тобто науки про вимiрювання, яка включає як теоретичні, так і практичні аспекти вимірювань у всіх галузях науки і техніки.

Основними проблемами метрології є такі:

• загальна теорiя вимiрювань;

• одиницi фiзичних величин та їхні системи;

• методи та засоби вимiрювальної техніки;

• методи визначення точностi вимiрювань;

• основи забезпечення єдностi вимiрювань та однаковостi засобiв вимiрювальної техніки;

• еталони та зразковi засоби вимiрювальної техніки;

• методи передавання розмiрiв одиниць вiд еталонiв або зразкових засобiв вимірювальної техніки до робочих засобів вимiрювальної техніки.

Метрологія поділяється на теоретичну, прикладну та законодавчу.

Теоретична метрологiя - роздiл метрології, присвячений загальним теоретичним проблемам: теорії вимiрювань, методам оброблення результатiв вимiрювань з метою оцiнювання їх точностi, теорiї величин i одиниць, теорiї вiдтворення i передавання розмiрiв одиниць та iн.

Прикладна метрологiя - роздiл метрології, що розглядає застосування метрології в практичних вимiрюваннях i забезпечення єдностi вимiрювань.

Законодавча метрологiя - частина метрології, що містить законодавчі акти, правила, вимоги та норми, які регламентуються і контролюються державою для забезпечення єдності вимірювань.

Метрологiя, як i будь-яка iнша наука, виникла та розвинулась пiд впливом практичних потреб суспiльства. З розвитком суспільства і особливо прискоренням науково-технiчного прогресу перед метрологiєю постають новi, дедалі складнiші завдання. Зокрема першочергове завдання метрології – пiдвищити точність та надiйність приладiв, що використовуються у процесi виробництва, облiку та контролю якостi продукції, якi значною мiрою пiдвищують ефективність виробництва. Зрозумiло, що розв’язати це завдання можна лише шляхом удосконалювання метрологічного забезпечення науки й техніки  взагалi.

Зміст     1.2 Основнi та похiднi фiзичнi величини й одиницi. Розмiрностi фiзичних величин

Зв’язки мiж фiзичними величинами, що виражаються рiвняннями типу (1.1), є не випадковими, а закономiрними, тому що вони за допомогою математичних символiв об’єктивно вiдтворюють взаємний зв’язок мiж рiзними формами руху матерії. Справді, фiзичний закон звичайно виражається таким рiвнянням зв’язку мiж фiзичними величинами:

 f(x₁, x₂ ,..., x_m) = 0,            (1.3)

де x₁, x₂, ..., x_m  - деякi фiзичнi величини;. f(x₁ ,x₂, ..., x_m)  - функцiя m змiнних..

Досить часто рiвняння (1.3) можна записати у виглядi  

x_m = f₁(x₁, x₂, ..., x_m-1),            (1.4)

де х_m - визначена в кожному конкретному випадку величина. Зауважимо, що в рівняннях (1.3) або (1.4) додавати чи віднімати можна лише однорідні величини. Неоднорідні величини A i B перемножують і ділять за правилами алгебри:

де добуток {A}{B} - числове значення {AB} величини AB; добуток [A][B] - одиниця [AB] величини AB; частка {A}/{B} - числове значення {A/B} величини A/B; частка [A]/[B] - одиниця [A/B] величини A/B.  Наприклад, швидкість v частинки, яка рухається рівномірно і прямолінійно, задається рівнянням v=l/t, де l - шлях, який подолала частинка за проміжок часу t. Якщо частинка подолала шлях l=6 м за час t=2 с, то її швидкість дорівнює 

v = l/t= (6 м)/(2 с) = 3 м/с.

Розрізняють два типи фізичних рівнянь: для величин, де символи величин позначають їхні значення, s для числових значень величин.

Рівняння для числових значень величин найчастіше є емпіричними формулами, отриманими безпосередньо у фізичному досліді, а їхній вигляд залежить від вибору одиниць. Одиниці всіх величин, використаних у таких рівняннях, мають бути чітко визначені в ньому самому або в контексті.

Рівняння для величин не залежать від вибору одиниць, тому саме їм треба завжди надавати перевагу.

Наприклад, якщо в досліді шлях вимірювали в метрах, час - у секундах, а швидкість - у кілометрах за годину, то емпірична залежність  

{v}км/год = 3,6{l}м/{t}с

є рівнянням для числових значень величин, де числовий множник 3,6 отримано як наслідок особливого вибору одиниць величин; у разі іншого вибору одиниць цей множник буде іншим.

Співвідношення v=l/t є рівнянням для величин, і його вигляд не залежить від вибору одиниць довжини, часу та швидкості.

Сукупнiсть фiзичних величин, взаємопов’язаних рівняннями, які виражають закони природи  або визначають нові величини, утворює систему фiзичних величин.

З метою аналiзу закономiрних зв’язкiв мiж фiзичними величинами, що перебувають у функцiональнiй залежностi одна вiд одної, величини умовно подiляють на основні та похiднi.

Основною (фiзичною) величиною називається фiзична величина, що входить у систему фізичних величин i прийнята за незалежну вiд iнших величин цiєї системи. Прикладами таких величин є довжина l,  маса m та час t.

 Похiдною (фiзичною) величиною  називається величина, що входить у систему величин та визначається через основнi величини цiєї системи. Такою величиною в механiцi буде, наприклад, швидкiсть, якщо довжину та час обрано як основнi величини системи.

Вибiр основних величин дозволяє визначати розмiрнiсть решти величин, що входять до системи.

Розмiрнiсть фiзичної величини - це вираз, що вiдображує її зв’язок з основними величинами системи величин, вона є умовним символом фізичної величини в даній системі величин.

Розмiрнiсть фiзичної величини визначає формула розмiрностей, загальний вигляд якої встановлюється такою теоремою.

Теорема 1. Розмiрнiсть фiзичної величини є добутком розмiрностей основних величин, пiднесених до відповiдних степенiв.

Доведення [67-70] цієї теореми ґрунтується на головній метрологічній вимозі, що висувається до будь-яких вимірювань: відношення чисел, за допомогою яких вимірюються два зразки фізичної величини, як основної, так і похідної, має не залежати від розміру основних одиниць, якими користувалися за умов цих вимірювань. Ця вимога "абсолютного значення відносної величини" є цiлком природною, бо відтворює той факт, що, коли, наприклад, довжина однiєї лiнiйки втричi перевищує довжину другої або сила струму в одному електричному колі вдвічі менша, ніж в  другому, тоді цi твердження мають виконуватися завжди за будь-якого вибору одиниць фiзичних величин вiдповiдно довжини та сили струму. У противному разi взагалi неможливо отримати об’єктивнi результати вимiрювань, оскільки сам процес порiвнювання з мiрою  стає невизначеним.

З теореми 1 випливає: якщо похідна величина z пов’язана з основними величинами x, y, … рівнянням зв’язку

z = f(x, y, …), 

то завжди має місце рівняння:

,           (1.5)

де С – стала; p₁, p₂,... – показники степенів.                          

Використовуючи (1.1) та (1.5), отримаємо рiвняння зв’язку мiж числовими значеннями величин

            (1.6)

  та рiвняння зв’язку між їхніми розмірами

             (1.7)

Зауважимо, хоча це й не випливає з теореми 1, що показники степенів - числа p₁, p₂,... - завжди виявляються рацiональними. Цi показники степеня, що визначають розмiрнiсть похiдної величини, називаються показниками розмiрностi фiзичної величини. Iнодi розмiрнiстю похiдної величини z неправильно називають сукупнiсть зазначених показникiв степеня.

Величина, в розмiрностi якої, принаймні одна з основних величин пiднесена до степеня, що не дорiвнює нулю, називається розмiрнісною фiзичною величиною.

Розмiрностi фiзичних величин позначаються великими лiтерами латинського алфавiту прямим шрифтом. Наприклад, якщо в механiцi як основнi величини обрати довжину, масу та час, то їхні розмiрностi позначають лiтерами вiдповiдно L, M, T.

Розмiрнiсть величин позначається символом dim  (вiд лат. dimension - розмiр, розмiрнiсть, вимiрювання). Тодi, наприклад, у системi механiчних величин L, M, T розмiрнiсть швидкостi можна одержати з формули швидкостi рiвномiрного прямолiнiйного руху: v = l/t. Вона  виражатиметься спiввiдношенням

dim v = LT^-1.

У даному випадку розмiрнiсть будь-якої фiзичної величини z позначатиметься формулою

dim  z = L^pM^qT^r, 

де p, q, r - рацiональнi числа.

Безрозмiрнісною фiзичною величиною називається величина, у розмiрності якої всі степенi розмірностей основних величин дорівнюють нулю. Зауважимо, що величина, яка є безрозмiрнісною в однiй системi величин, може мати розмiрнiсть в iншiй.

За допомогою спiввiдношення (1.7) можна також подiлити одиниці фiзичних величин на основні та похiднi, що, як i відповідні до них фiзичнi величини, утворюють  систему одиниць. Іншими словами, система одиниць - це сукупність одиниць певної системи фізичних величин.

Основною одиницею (системи одиниць) називається одиниця основної фiзичної величини в певній системi одиниць. Наприклад, у системi  одиниць СГС, що вiдповiдає системi величин з основними величинами довжини, маси та часу, основними одиницями є сантиметр, грам, секунда.

Похiдною одиницею (системи одиниць) називається одиниця похiдної фiзичної величини в певній системi одиниць. Вона утворюється згідно з рiвнянням, що пов’язує її з основними одиницями або з основними та вже визначеними похiдними одиницями. Зазначенi визначальнi рiвняння для похiдних одиниць, взагалi кажучи, обираються довiльно. Але перевагу наддають найпростішим рiвнянням, в яких фiзичнi величини пов’язанi мiж собою лише операцiями множення або дiлення, а коефіцієнт пропорційності дорівнює числу 1. Наприклад, в СІ одиниця iндуктивностi генрi впроваджується за допомогою рiвняння зв’язку мiж iндуктивністю L, потокозачепленням Y та силою струму I.

L = Y/I,

хоча, у принципi, з тiєю самою метою можна використати виразу для е.р.с. самоіндукції :

Якщо похiдну одиницю пов’язано з іншими одиницями системи рiвнянням, в якому числовий коефiцiєнт дорiвнює числу 1, то вона називається когерентною одиницею (системи одиниць).

Прикладами когерентних одиниць можуть бути: одиниця швидкостi v 1 м/с, яку утворено за рiвнянням мiж одиницями

[v] = [l]^.[t]^-1,

де [l] = 1 м, [t] = 1 с, або одиниця iндуктивностi L 1 генрi, що визначається рiвнянням

[L] = [Y]^.[I]^-1,  

де [Y] = 1 Вб, [I] = 1 А.

Системою одиниць (фiзичних величин) називається сукупнiсть одиниць певної системи фiзичних величин. Тоді системною одиницею фiзичної величини є основна чи похiдна одиниця цієї системи одиниць.

Одиниця фізичної величини, що не належить до даної системи одиниць, називається позасистемною.

Одиниці величин, що належать до однієї системи одиниць, можуть бути системними чи позасистемними щодо іншої. Наприклад, грам – основна одиниця

 маси системи СГС – є системною одиницею в межах СІ (частинною від кілограма), але позасистемною щодо системи MKГСС. Такі одиниці іноді називають іншосистемними щодо обраної системи одиниць.

Існують також одиниці величин, що не належать до жодної системи одиниць. Це так звані спеціальні позасистемні одиниці, наприклад, доба, година, хвилина.

Когерентною системою одиниць (фiзичних величин) називається система одиниць, усі похiдні одиниці якої когерентні.

У межах когерентної системи можливе введення кратних і частинних одиниць вiд системних одиниць.

Кратною одиницею (фізичної величини) називається одиниця фізичної величини, яка в цiле число разiв перевищує одиницю, від якої вона утворюється, а  частинною одиницею (фізичної величини) - одиниця фізичної величини, яка в цiле число разiв менша від одиниці, від якої вона утворюється.

Звичайно, назви кратних і частинних одиниць одержують доданням вiдповiдних префiксiв до назв вихiдних одиниць з урахуванням правил, що розглядатимуться далі. Цi одиницi за визначенням не є когерентними, їх запроваджено для забезпечення бiльшої зручностi при виконанні вимiрювань фiзичних величин і розрахункiв.

Нині кiлькість систем одиниць, що використовують у науковiй і технiчнiй практицi, істотно зменшилась унаслiдок широкого впровадження Мiжнародної системи одиниць. Проте в рядi випадкiв, наприклад у теорії атомного ядра, застосування iнших систем одиниць є більш слушним порiвняно із СІ.

У ранiше надрукованiй науковiй і технiчнiй лiтературi широко використовувалися рiзні системи одиниць. Крiм того, багато  систем одиниць на практицi застосовується i нині. У зв’язку з цим досі  актуальним залишається питання про перехід вiд одиниць однiєї системи до одиниць iншої системи.

Нехай основними одиницями однієї системи є x₁, x₂, x₃, а другої - y₁, y₂, y₃ (змiна кiлькостi основних одиниць нiчого не змiнює в подальших мiркуваннях). Припустимо, що показниками розмiрностi y₁ у системi одиниць (x₁, x₂, x₃) є p₁, p₂, p₃, розмірності y₂ – q₁, q₂, q₃, а розмірності y₃ – r₁, r₂, r₃. Тодi виконуватимуться рiвностi типу (1.5)

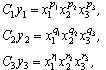
де C₁, C₂, C₃ - числовi множники. Пiсля їх логарифмування матимемо        

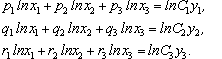
Ці рiвняння мають розв’язок, якщо

        Iнакше кажучи, достатньою умовою можливостi переходу вiд однієї системи одиниць до iншої є нерiвнiсть нулю визначника, складеного з показникiв розмiрностей основних величин однiєї системи в іншій системi.

          Якщо зазначена умова виконується, то легко відшукати вирази для x₁, x₂, x₃. Наприклад, а вирази для x₂ та x₃ одержують з наведеної рівності коловим переставленням. Очевидно, що необхiдною умовою можливостi розглядуваного переходу є збiг числа основних одиниць в обох системах.

Зміст      1.3 Принцип однорiдностi щодо розмірностей. П -теорема

 Величини, що входять у рiвняння фiзики, можуть бути змiнними та сталими. Змiннi величини можуть мати різнi числовi значення в рiзних станах фiзичного об’єкта, сталі не змінюють свого значення для об’єкта, що розглядається. У бiльшостi випадкiв ця класифiкацiя вiдносна, тобто величини, змiнні для одного фiзичного об’єкта, можуть бути сталими для iншого, i навпаки. Проте є й такі фізичні сталi, якi в межах наших знань про Природу не змінюють своїх значень за будь-яких обставин. Вони називаються фундаментальними  сталими (див. гл. 5). До них належать, наприклад, швидкiсть свiтла,  стала Планка та ін.

Як змiннi, так i сталi величини можуть бути розмiрнісними та безрозмiрнісними. При цьому величина безрозмірнісна в однiй системi величин може бути розмірнісною в iншiй, і навпаки. Це, здавалося б, очевидне твердження є далеко не тривiальним i дає змогу сформулювати  другу основну теорему аналізу розмiрностей, яку часто називають П-теоремою [67-70].

Аналіз розмірностей - метод визначення функційних зв’язків між фізичними величинами на ґрунті їхньої розмірності. Цей метод є суто якiсним i не дає змоги зробити остаточні висновки щодо точного вигляду рівнянь фiзики. Тому при його вивченні та використання безрозмiрнiсні сталi величини (тобто просто числа) не розглядаються. Таким чином, усi результати, одержанi за допомогою аналiзу розмiрностей, є справедливими з точнiстю до числового множника.

Будь-яка одержана експериментально або теоретично фiзична закономiрнiсть являє собою функцiйне спiввiдношення мiж змiнними та сталими розмiрнісними та безрозмiрнісними величинами i в загальному випадку може бути записана у виглядi рiвностi (1.3). Зважаючи на зазначене обмеження аналізу розмірностей, усi x_i з (1.3) слiд вважати або змінними величинами довільної розмірності, або розмірнісними сталими величинами. Функцiйне рiвняння (1.3) називається повним, якщо воно є коварiантним [66] щодо будь-якої змiни розмірiв основних величин. Зрозумiло, що після переходу в iншу систему основних величин, вигляд спiввiдношення (1.3) може змiнитися.

Вимога повноти спiввiдношення (1.3) не є жорстким обмеженням. Відповідно до сформульованого Фур’є у його класичнiй працi "Аналітична теорiя теплоти" [85] принципу однорiдностi щодо розмiрностей усi доданки, що входять до фiзичних рiвнянь, повиннi мати однаковi показники відповідних розмірностей. Тоді згiдно з теоремою 1 усi фiзичнi рівняння типу (1.3) є повними.

При цьому з розгляду вилучають лише ті рiвняння, що коректнi математично, але не мають фiзичного змiсту. Наприклад, протікання струму силою I через резистор з опором R при напрузi U на його кiнцях описується законами Ома та Ленца-Джоуля:

IR = U,             I²R = P,

де P - теплова потужнiсть. Якщо переписати цi рiвняння у виглядi

IR – U = 0,             I²R – P = 0

та підсумувати їх, то дістанемо

IR – U = I²R – P.            (1.8)

У системi основних величин (довжина, маса, час, сила струму), яка  тут використовується, спiввiдношення (1.8) є математично коректним, але принцип однорідностi щодо розмірностей забороняє його використання, тому що розмiрностi лiвої та правої частин не збігаються:

dim (IR) = dim U = L²MT^-3I^-1,

dim (I²R) =dim P = L²MT^-3,

де I - розмiрнiсть сили струму, яка є основною величиною Мiжнародної системи одиниць.

На пiдставi принципу розмiрнісної однорiдностi 1814 року Е.Бекiнгем [86] довів другу теорему аналізу розмiрностей (П-теорему).

Теорема 2. Якщо є повне спiввiдношення мiж фiзичними величинами

j(x₁, x₂, ..., x_m) = 0            (1.9)

то в такiй самiй системi основних величин можна знайти спiввiдношення, яке має вигляд

Ф(П₁, П₂, ..., П_n) = 0            (1.10)

де П_j (j=1,...n)незалежнi безрозмiрнiсні величини (П-комплекси), що являють собою добутки степенiв аргументiв x_i. Число n дорiвнює

n = m – k,            (1.11)

де k - максимально можлива кількість величин x_i, з яких не можна створити безрозмiрнісну величину. Такi величини мають незалежнi розмiрностi.

У бiльшостi випадкiв k дорiвнює мiнiмально можливому числу r незалежних основних величин, за допомогою яких можна визначити розмірності всіх величин xi. Проте, як це доведено у роботi [58],  y загальному випадку

k Ј r.            (1.12)

Наведена теорема 2 є основним iнструментом аналізу розмiрностей. З її допомогою завжди можна будь-яке фiзичне спiввiдношення мiж розмірнісними величинами перетворити на спiввiдношення мiж безрозмiрнісними величинами, тобто "звести до безрозмiрнісного вигляду". Це, як правило, зменшує кiлькiсть змiнних, що входять у спiввiдношення, і спрощує дослідження зазначеного спiввiдношення.

Найефективніше застосовувати П-теорему тоді, коли  k = m – 1, тобто коли всі x_i, крім x_m, мають незалежні розмірності.

Зміст      1.4 Методи фiзичних досліджень, якi ґрунтуються на аналізi розмiрностей.  Доповнення Хантлi

Важливою проблемою, що постає при застосуванні аналізу розмірностей, є вибір кiлькостi та виду основних величин. Не спиняючись на методологічних питаннях, що постають при цьому (див., наприклад, [67; 68]), розглянемо тiльки практичний аспект цiєї проблеми, вважаючи, що "критерiй вибору одиниць є суто прагматичним" [68]. Під таким кутом зору вибір основних величин (або одиниць) визначається природою фiзичного явища, що вивчається, та умовою мiнімальної кiлькостi розмiрнісних сталих. Останнє пов’язане з тим, що, коли число розмiрнісних сталих, якi фiгурують у розв’язку, перевищує або дорiвнює числу змiнних величин, то кiлькiсть П-комплексiв перевищує або дорівнює кiлькість змiнних величин i використовувати П-теорему немає сенсу.

При дослідженнi механiчних явищ достатньо використати три незалежні основнi величини – довжину, масу та час, що мають розмірності відповідно L, M, T.

Взагалi кажучи, цими самими величинами можна обiйтись при вивченні термодинамiчних i навiть електромагнітних процесів. Проте на практицi до основних величин зручно ввести температуру (розмiрнiсть Q) для опису теплових явищ і силу струму (розмiрнiсть I) для опису електромагнiтних явищ. Це спричинює появу у фiзичних рівняннях двох "розмiрнісних" сталих: сталої Больцмана k_B та магнітної сталої m₀ (електрична стала e₀ визначається як e₀=1/(m₀·с²), де с - швидкiсть свiтла у вакуумi).

Окрiм зазначених розмiрнісних сталих при описі різних класів фiзичних явищ з’являються так звані фундаментальні константи. До них належать: у механiцi - гравiтацiйна стала G або пов’язана з нею величина прискорення вiльного падiння g; в електродинамiцi - швидкість свiтла с у вакуумi; у квантовiй фiзицi - стала Планка h та ін.

Остаточно вирішити, якi розмірніснi сталi слiд або не слід включати в рiвняння, що описує даний процес, можна лише пiсля ретельного аналізу i значною мiрою, iнтуїтивно [67-70]. При цьому слiд пам’ятати, що збільшення числа основних величин на одиницю приводить до появи нової розмiрної сталої.

Число основних величин може бути будь-яким. Кожне зменшення числа основних величин пов’язане з тим, що одну з розмiрнісних або фундаментальних констант беруть як безрозмiрнісну. Iнакше кажучи, цю сталу використовують для вираження розмiру тiєї чи iншої фiзичної величини. Наприклад, вважаючи безрозмiрнісною сталу тяжiння G i виходячи зі закону всесвiтнього тяжiння, з основних механiчних величин не важко вилучити масу m. При цьому її розмiрнiсть, виражена через довжину та час, має вигляд

dim m = L³T^-3.

Далi, вважаючи безрозмiрнісною швидкiсть свiтла с у вакуумi, з числа основних величин можна вилучити довжину l (тепер її розмірнiсть має вигляд [l] = T²). Нарештi, всi фiзичнi величини можна зробити безрозмiрнісними, якщо вважати всi фiзичнi сталi також безрозмiрнісними. Цю iдею покладено до підвалин так званих "природних систем одиниць". Проте на практицi зручнiше в різних розділах фiзики впроваджувати новi основнi величини або навiть набори основних величин, узгоджуючи їх впровадження з фiзичною важливiстю та частотою використання тих чи інших величин при описаннi дослiджуваного класу явищ.

З погляду аналізу розмiрностей зменшення числа основних величин лише зменшує його "роздiлювальну здатнiсть", тобто звужує коло явищ, якi можна дослiджувати за допомогою теорем цього аналізу. Набагато цiкавішим є зворотний випадок – збiльшення числа основних величин. Це дає змогу iстотно розширити сферу застосування аналiзу розмiрностей. Проте, як вiдомо, впровадження нової основної величини спричинює появу нової розмірнісної сталої, тобто кiлькість m змінних та кількість k незалежних безрозмiрнісних комплексiв збiльшуються на одиницю. Iнакше кажучи, число n = m – k залишається попереднім та сфера застосування П-теореми не розширюється.

Цiкавий вихiд з цього становища знайшов Г.Хантлi [68]. Вiн запро­понував спосiб  "розкладання" основних величин – довжини та маси – на простiші складовi. Iдея доповнення Хантлi полягає в тому, щоб при розглядi фiзичних систем розрiзняти довжини, що вимiрюються за рiзними напрямами (l_x, l_y, l_z), та вiдповiдно впровадити "векторнi розмiрностi" (L_x, L_y, L_z). Аналогiчно, слiд розрiзняти масу як кiлькiсть речовини (dim m = M_m) та масу як мiру iнерції (dim m = M_i). За допомогою такого пiдходу одержано новi результати в рядi задач механiки та теорії теплоти.

Основний змiст аналiзу розмiрностей зводиться до задоволення вимоги незалежностi зв’язку мiж фiзичними величинами вiд вибору одиниц, що рiвнозначно вимозi рiвностi розмiрностей у правiй та лiвiй частинах будь-якого рiвняння. Саме ця обставина уможливлює застосування аналізу розмiрностей для розв’язання багатьох практичних задач. Особливостi такого застосування аналiзу розмiрностей розглянуто, наприклад, у навчально-довiдковому посiбнику [48] та інших працях   [66 - 78].

Важливе наукове значення зазначеного методу полягає в тому, що за його допомогою можна встановити основнi риси закономiрних зв’язкiв мiж фiзичними величинами, якi характеризують тi чи iншi процеси, тобто вигляд вiдповiдних рiвнянь фiзики.

Аналiз розмiрностей як фiзичний метод дослiдження використо­вується в рiзних галузях фiзики й технiки.

Деякi його застосування досить вiдомi й поширені. До них належать вiдновлення забутої фiзичної формули, якщо відомi розмірностi величин, які входять в неї; перевiрка рiвнянь і формул щодо розмiрнісної однорiдності доданкiв; визначення коефiцiєнтiв переведення одиниць фiзичних величин з однiєї системи одиниць в iншу.

Проте набагато вагоміiшi результати аналiз розмiрностей дає як евристичний метод (евристика - від грецьк. heuricko (знаходження) - мистецтво відшукування iстини). Прямим наслiдком теореми 1 є можливiсть дослiдження великомасштабних явищ і процесiв за допомогою невеликих моделей, подiбних до оригiналу в розумінні розмiрностей величин, що описують ці моделі. Особливо широко такий метод подiбностi застосовується в механiцi й гiдродинамiцi [70].

За допомогою другої теореми аналiзу розмiрностей можна видокремити з усього набору фiзичних величин, які визначають процес або явище, що вивчається, тi їхні безрозмiрнісні комбiнації, якi насправдi слiд вимiрювати дослідно. Отже з’являється можливiсть свiдомого планування експерименту, що забезпечує повну iнформацiю про досліджуваний об’єкт за умови мiнімiзації зусиль, які витрачаються на вимiрювання. 

Нарештi, аналiз розмiрностей дає змогу одержувати частиннi роз’язки задач тоді, коли їхнє повне математичне розв’язання важко чи навiть неможливо виконати.

У всіх цих трьох випадках схеми застосування аналiзу розмiрностей мають однаковi початковi етапи.

Насамперед будується фiзична модель досліджуваного процесу, тобто з’ясовується, якого класу явища (механічні, електромагнітнi тощо) при цьому вiдбуваються та якими фiзичними величинами можна повністю описати даний процес. На цьому етапi велику роль вiдіграють iнтуїція та досвiд дослідника, його спроможнiсть збагнути суть взаємних зв’язкiв і закономiрностей мiж величинами.

Потім обираються основні фізичні величини, зручнi для застосування в даному конкретному випадку (нині рекомендується використовувати основнi величини СІ) i складається таблиця фiзичних величин із  зазначенням їхніх назв, позначень і розмiрностей в обраній системi величин (одиниць). До цієї самої таблиці слід включити розмiрні сталі, якi можуть з’явитись у розв’язку. Побудувати таблицю основних змiнних задачi особливо легко, якщо задачу сформульовано математично, навіть якщо неможливо одержати її точний розв’язок. На цьому ґрунтуються методи фракцiйного аналiзу, описані, наприклад, у [69].

Набір змiнних, включених у таблицю, має бути мiнімальним i разом з тим таким, щоб через їхні розмірностi можна було виразити розмірності всіх iнших змiнних, якi виникають при описанні дослiджуваної фiзичної системи. Такий набір можна назвати системою визначальних параметрiв [70].                                        

Подальшi кроки дослідження різняться залежно вiд його кінцевої мети. Вкажемо лише, що в усіх випадках вельми плiдним є залучення мiркувань, що випливають з властивостей симетрії та лiнійностi системи, яка вивчається, а також з математичного формулювання задачi (якщо воно вiдомо) й асимптотичних властивостей функцiй, що входять в це формулювання.

Для подальшого ознайомлення з теорією і практикою застосування загальних і вузькофахових методів аналізу розмірностей можна рекомендувати такі праці, як [66-71; 80].

Зміст      1.5 Зведення основних практичних правил теорії розмірностей

1 Аналiз розмiрностей формул не може допомогти у відшуканнi значень безрозмiрнісних сталих.

2 Виведення розрахункових формул під час розв’язування фiзичних та iнженерних задач часто пов’язане з досить громiздкими алгебраїчними перетвореннями. Це, у свою чергу, може спричинити помилки в кiнцевому виразi. Аналiз розмiрностей одержаного спiввiдношення дає змогу одразу встановити його "фiзичну коректнiсть" (з точнiстю до безрозмiрнісного множника чи доданка) щодо принципу розмiрної однорiдностi.

Виконуючи такі перевiрки, слiд також пам’ятати, що у фiзичних формулах "пiд знаком функцiї" cos(x), sin(x), exp(x), ln(x) та ін може стояти лише безрозмiрнісна величина х.

3 Якщо всi величини у досліджуваній формулi мають однакову фізичну природу (тiльки механiчнi, механiчнi й тепловi, тiльки електричнi тощо), то використання одиниць величин замiсть їхніх розмiрностей є цiлком виправданим, а iнодi навiть простiшим.

4 Принцип розмiрної однорiдностi мають задовольняти не тiльки алгебраїчнi, а й диференцiальнi та iнтегральнi рiвняння фiзики. Перевiряючи їх, слiд пам’ятати, що операцiя iнтегрування, яка позначається знаком iнтеграла, не змiнює розмiрнiсть пiдiнтегральної величини, а розмiрнiсть диференцiала деякої величини збігається з розмiрнiстю цiєї самої величини.

У визначеному iнтегралi розмiрностi його верхньої  та нижньої меж мають збігатися мiж собою i з розмiрнiстю величини, що стоїть пiд знаком диференцiала в пiдiнтегральному виразі.

5 Комплекснi фiзичнi величини взагалi не мають розмiрностi, оскільки це поняття внаслідок їх принципової невимірюваності до них не може бути застосоване. Умовно розмiрнiсть комплексної фiзичної величини дорiвнює розмiрностi її модуля. Розмiрностi модуля, дiйсної та уявної частин комплексної фiзичної величини мають збігатися. Фаза комплексної величини є безрозмiрнісною.

6 При аналiзi розмiрнісної однорiдностi рівнянь, у всі доданки яких деяка величина входить в однаковому степені, можна взагалi не звертати уваги на розмiрнiсть такого однорiдного множника (тобто вважати цю величину умовно безрозмірнісною), тому що це нiяк не вiдiб’ється на кiнцевому результатi.

7 У процесі аналiзу розмiрностей рiвнянь фiзики часто виникає питання щодо розмiрностi нуля, який у багатьох випадках розташований у правiй частинi рiвнянь. Слiд пам’ятати, що нулю можна надавати будь-яку розмiрнiсть.

8 Розмiрнiсть векторної фiзичної величини завжди збігається з розмiрнiстю її модуля. Розмiрностi складових вектора завжди збігаються мiж собою i з розмiрнiстю модуля цiєї величини. Це твердження залишається правильним і для чотиривимiрних векторiв, що використовуються в релятивній фiзицi.

9 Компоненти тензорних фiзичних величин повинні мати однакову розмірність.

10 Рівняння між числовими значеннями величин є правильними лише тодi, коли використовуються саме тi одиницi, якi вказано для кожної з величин, що включені в них. У цих формулах недопустимо змiнювати розмiрiв величин, оскільки це приводить до змiни числового множника.

11 Використовуючи методи теорії розмірностей для розв’язання задач статистичної фiзики i термодинамiки, згiдно зi стандартом СІ слiд обов’язково до довжини, маси та часу долучити ще одну основну величину - температуру T, що має розмiрнiсть Q. У розв’язках цих задач має з’явитися також нова розмiрнісна стала – стала Больцмана k_B.

12 Дослiдження задач, пов’язаних з електричними полями, в разі використання СІ потребує впровадження нової основної величини - сили струму I,  що має розмiрнiсть I, і водночас нової розмiрнісної сталої - електричної сталої e_o. У задачах, де фiгурують магнiтнi поля, завжди з’являється або магнiтна стала m_o, або швидкiсть свiтла c у вакуумi.

13 Критерiєм подiбностi  називається безрозмiрнісна величина (П-комплекс), яка є деякою середньою мiрою вiдношення iнтенсивностей двох фiзичних ефектiв, суттєвих для дослiджуваного процесу або явища. Якщо в попередньому аналiзi, тобто протягом постановки задачі, правильно враховано всi особливостi системи, що вивчається, то П-теорема гарантує можливiсть визначення всіх істотних для цієї задачi критерiїв подiбностi. Найчастіше вживані критерії подібності мають назву характеристичних чисел (див. гл. 5).

Закон подібностi констатує:

Двi фiзичнi системи подiбнi, якщо критерiї подiбностi, якi  їх описують, попарно дорiвнюють один одному за умови, що використовуваний набiр критерiїв для кожної системи має достатню повноту.

Остання обставина створює основну перешкоду при застосуваннi теорiї подiбностi, через те що апрiорi нiколи не зрозуміло, чи вичерпанi пiд час постановки задачi всi iстотнi характеристики досліджуваної системи.

 14 Знання критерiїв подiбностi системи дає змогу iстотно спростити планування експерименту, в якому вона вивчається, тому що багато функцiйних зв’язкiв мiж її параметрами вже встановлено, тобто немає потреби дослiджувати вплив на процеси в системі кожного параметра окремо.

15 За наявності набору критерiїв подiбностi можливе фiзичне моделювання, тобто такий фiзичний експеримент, в якому змiнено масштаби або навiть фiзичну природу явища, але збережено незмiнними критерiї подібності порівнюваних систем.

Єднiсть основних принципiв і алгоритмiв, якi застосовують до явищ зовсiм рiзної фiзичної природи, дозволяє встановити критерiї подiбностi, а отже, і моделювати одну систему за допомогою дослідження властивостей фiзично iншої системи. Особливо корисна ця можливiсть при реалiзацiї числового (комп’ютерного) моделювання, яке повністю ґрунтується на принципi, сформульованому Р.Фейнманом [88]:

Однаковi рiвняння - однаковi розв’язки.

Розв’язки, одержанi внаслiдок числового моделювання, - це завжди числа, тобто безрозмiрнісні величини, якi без зазначення характерних розмiрiв дослiджуваної системи малоінформативні. Iнакше кажучи, фiзично змiстовний результат комп’ютерного експерименту завжди складається з власне числового результату та набору значень критерiїв подiбностi для дослiджуваної системи. Зазначимо, що знання критерiїв подібності дає змогу зробити висновок про можливiсть фiзичного моделювання однiєї системи за допомогою iншої, навіть не вдаючись до послуг комп’ютера.

  [1]  Тут і далі у цьому підрозділі терміни, визначення яких подано відповідно до Закону України "Про метрологію та метрологічну діяльність", підкреслено. Якщо визначення терміна наведено в стандарті [4], то такий термін виділено курсивом.Усі інші терміни, що не увійшли в зазначений Закон або стандарт [4], надруковано звичайним шрифтом. Узята в круглі дужки частина терміна може бути вилучена в разі використання його у документах із стандартизації.